首语
- 上一篇:数据结构与算法(图)
图的遍历
- 图的遍历和树的遍历相似,我们希望从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这个过程就叫做图的遍历(Traversing Graph)。
深度优先遍历
- 深度优先遍历(Depth_First_Search),也称为深度优先搜索,简称为DFS。
- 它从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。
代码实现
- 递归实现
/**
* 对外公开的深度优先遍历
*/
public void depthFirstSearch() {
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
System.out.println("被访问到了:" + i + "顶点");
depthFirstSearch(i);
}
}
isVisited = new boolean[vertexSize];
}
/**
* 图的深度优先遍历算法
* @param i
*/
private void depthFirstSearch(int i) {
isVisited[i] = true;
int w = getFirstNeighbor(i);
while (w != -1) {
if (!isVisited[w]) {
//需要遍历该顶点
System.out.println("被访问到了:" + w + "顶点");
depthFirstSearch(w);
}
w = getNextNeighbor(i, w);
}
}
/**
* 获取某个顶点的第一个邻接点
*
* @param index
* @return
*/
public int getFirstNeighbor(int index) {
for (int j = 0; j < vertexSize; j++) {
if (matrix[index][j] > 0 && matrix[index][j] < MAX_WEIGHT) {
return j;
}
}
return -1;//无邻接点
}
/**
* 根据前一个邻接点的下标来获取下一个邻接点
*
* @param v1 要找的顶点
* @param v2 表示该顶点相对于那个邻接点去获取下一个邻接点
* @return
*/
public int getNextNeighbor(int v1, int v2) {
for (int j = v2 + 1; j < vertexSize; j++) {
if (matrix[v1][j] > 0 && matrix[v1][j] < MAX_WEIGHT) {
return j;
}
}
return -1;
}
- 栈实现
public void dfs() {
// 初始化所有的节点的访问标志
for (int v = 0; v < visited.length; v++) {
visited[v] = false;
}
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < vexnum; i++) {
if (visited[i] == false) {
visited[i] = true;
System.out.print(vertices[i] + " ");
stack.push(i);
}
while (!stack.isEmpty()) {
// 当前出栈的节点
int k = stack.pop();
for (int j = 0; j < vexnum; j++) {
// 如果是相邻的节点且没有访问过.
if (arcs[k][j] == 1 && visited[j] == false) {
visited[j] = true;
System.out.print(vertices[j] + " ");
stack.push(j);
// 这条路结束,返回上一个节点.
break;
}
}
}
} // 输出二维矩阵
System.out.println();
pritf(arcs);
}
/**
* 输出邻接矩阵
*/
public void pritf(int[][] arcs) {
for (int i = 0; i < arcs.length; i++) {
for (int j = 0; j < arcs[0].length; j++) {
System.out.print(arcs[i][j] + "\t");
}
System.out.println();
}
}
广度优先遍历
- 广度优先遍历(Breadth First Search),也称为宽度优先搜索,简称为BFS。
- 类似于树的层序遍历,使用队列实现。
代码实现
public void broadFirstSearch() {
isVisited = new boolean[vertexSize];
for (int i = 0; i < vertexSize; i++) {
if (!isVisited[i]) {
broadFirstSearch(i);
}
}
}
/**
* 实现广度优先遍历(队列)
*
* @param i
*/
private void broadFirstSearch(int i) {
int u, w;
LinkedList<Integer> queue = new LinkedList<>();
System.out.println("被访问到了:" + i + "顶点");
isVisited[i] = true;
queue.add(i);//第一次把v0加到队列
while (!queue.isEmpty()) {
u = queue.removeFirst();
w=getFirstNeighbor(u);
while (w!=-1){
if (!isVisited[w]){
System.out.println("被访问到了:" + w + "顶点");
isVisited[w]=true;
queue.add(w);
}
w=getNextNeighbor(u,w);
}
}
}
最小生成树
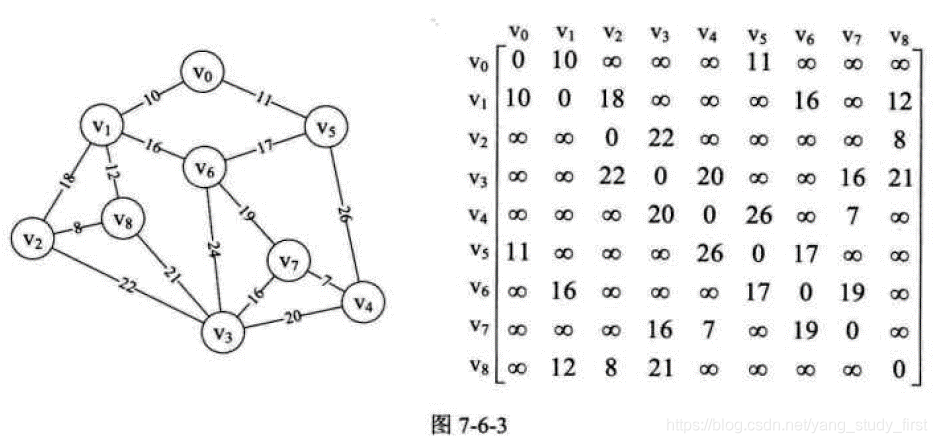
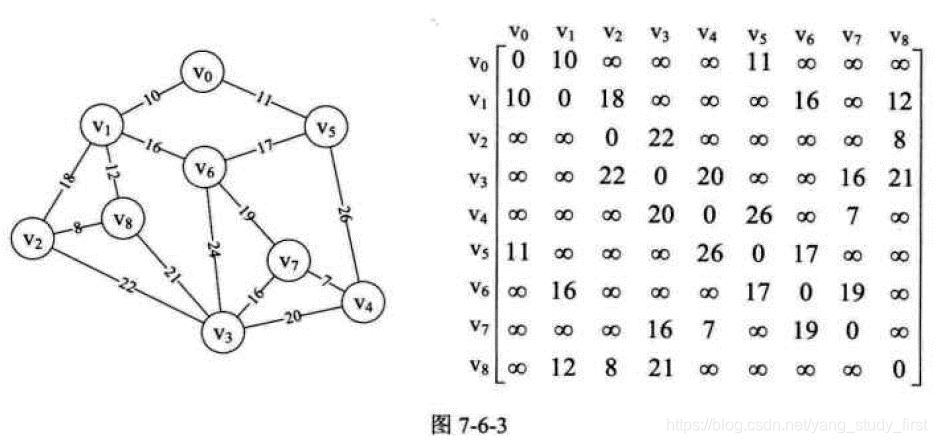
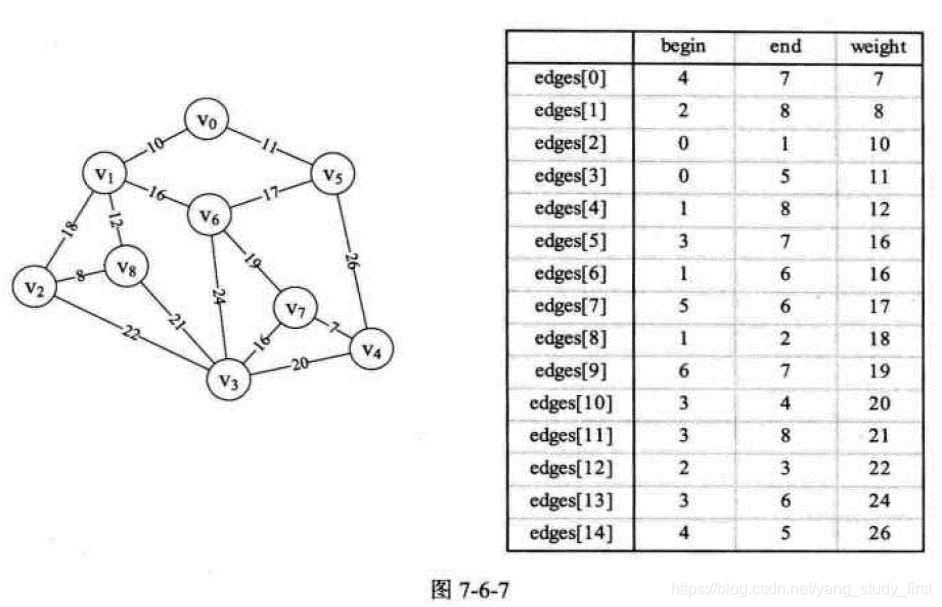
- 假设你是电信的实施工程师,需要为一个镇的九个村庄架设通信网络做设计,村庄位置大致如图, 其中Vo~V8是村庄,之间连线的数字表示村与村间的可通达的直线距离,比如Vo至V1就是10公里(个别如Vo与V6, V6与V8, V5与V7未测算距离是因为有高山或湖泊,不予考虑)。你们领导要求你必须用最小的成本完成这次任务。你说怎么办?
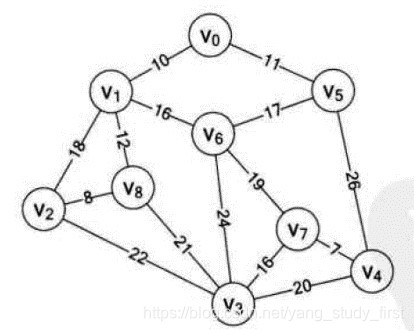
- 一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。我们把构造连通网的最小代价生成树。称为最小生成树。
- 找连通网的最小生成树,经典的有两种算法,普利姆算法和克鲁斯卡尔算法。
代码实现
- 普林姆算法
/**
* prim 普里姆算法
*/
public void prim(){
int[] lowcost=new int[vertexSize];//最小代价顶点权值的数组,为0表示已经获取最小权值
int[] adjvex=new int[vertexSize];//放顶点权值
int min,minId,sum=0;
for (int i=1;i<vertexSize;i++){
lowcost[i]=matrix[0][i];
}
for (int i=1;i<vertexSize;i++){
min=MAX_WEIGHT;
minId=0;
for (int j=1;j<vertexSize;j++){
if (lowcost[j]<min&&lowcost[j]>0){
min=lowcost[j];
minId=j;
}
}
System.out.println("顶点:"+adjvex[minId]+"权值:"+min);
sum+=min;
lowcost[minId]=0;
for (int j=0;j<vertexSize;j++){
if (lowcost[j]!=0&&matrix[minId][j]<lowcost[j]){
lowcost[j]=matrix[minId][j];
adjvex[j]=minId;
}
}
}
System.out.println("权值总和:"+sum);
}
- 克鲁斯卡尔算法
先构造一个只含 n 个顶点、而边集为空的子图,把子图中各个顶点看成各棵树上的根结点,之后,从网的边集 E
中选取一条权值最小的边,若该条边的两个顶点分属不同的树,则将其加入子图,即把两棵树合成一棵树,反之,若该条边的两个顶点已落在同一棵树上,则不可取,而应该取下一条权值最小的边再试之。依次类推,直到森林中只有一棵树,也即子图中含有 n-1 条边为止。
/**
* 克鲁斯卡尔算法最小生成树
*/
public void miniSpanTreeKruskal(){
int m,n,sum=0;
int[] parent=new int[edgeSize];//神奇的数组,下标为起点,值为终点
for (int i = 0; i < edgeSize; i++) {
parent[i]=0;
}
for (int i = 0; i < edgeSize; i++) {
n=find(parent,edges[i].begin);
m=find(parent,edges[i].end);
if (n!=m){
parent[n]=m;
System.out.println("起始顶点:"+edges[i].begin+"结束顶点:"+edges[i].end+"权值:"+edges[i].weight);
sum+=edges[i].weight;
}else {
System.out.println("第"+i+"边回环了!");
}
}
System.out.println("权值总和:"+sum);
}
/**
* 将神奇数组进行查询获取非回环的值
* @param parent
* @param f
* @return
*/
private int find(int[] parent, int f) {
while (parent[f]>0){
System.out.println("找到起点:"+f);
f=parent[f];
System.out.println("找到终点:"+f);
}
return f;
}
public void createEdgeArray(){
Edge edge0 = new Edge(4,7,7);
Edge edge1 = new Edge(2,8,8);
Edge edge2 = new Edge(0,1,10);
Edge edge3 = new Edge(0,5,11);
Edge edge4 = new Edge(1,8,12);
Edge edge5 = new Edge(3,7,16);
Edge edge6 = new Edge(1,6,16);
Edge edge7 = new Edge(5,6,17);
Edge edge8 = new Edge(1,2,18);
Edge edge9 = new Edge(6,7,19);
Edge edge10 = new Edge(3,4,20);
Edge edge11 = new Edge(3,8,21);
Edge edge12 = new Edge(2,3,22);
Edge edge13 = new Edge(3,6,24);
Edge edge14 = new Edge(4,5,26);
edges[0] = edge0;
edges[1] = edge1;
edges[2] = edge2;
edges[3] = edge3;
edges[4] = edge4;
edges[5] = edge5;
edges[6] = edge6;
edges[7] = edge7;
edges[8] = edge8;
edges[9] = edge9;
edges[10] = edge10;
edges[11] = edge11;
edges[12] = edge12;
edges[13] = edge13;
edges[14] = edge14;
}
class Edge{
private int begin;
private int end;
private int weight;
public Edge(int begin, int end, int weight) {
this.begin = begin;
this.end = end;
this.weight = weight;
}
}




