首语
二叉树的建立
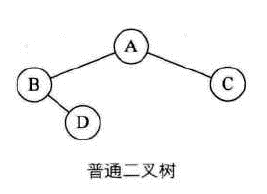
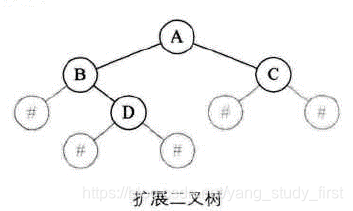
代码实现
/**
* 通过前序遍历的数据序列反向生成二叉树
* A
* B C
* D E # F
* # # # # # #
* <p>
* ABD##E##C#F##
*/
public void createBinaryTreePre(ArrayList<String> data){
createBinaryTree(data.size(),data);
}
public TreeNode createBinaryTree(int size, ArrayList<String> data) {
if (data.size() == 0) {
return null;
}
String d = data.get(0);
TreeNode node;
int index = size - data.size();
if (d.equals("#")) {
node = null;
data.remove(0);
return node;
}
node = new TreeNode(index, d);
if (index == 0) {
//创建根节点
root = node;
}
data.remove(0);
node.leftChild = createBinaryTree(size, data);
node.rightChild = createBinaryTree(size, data);
return node;
}
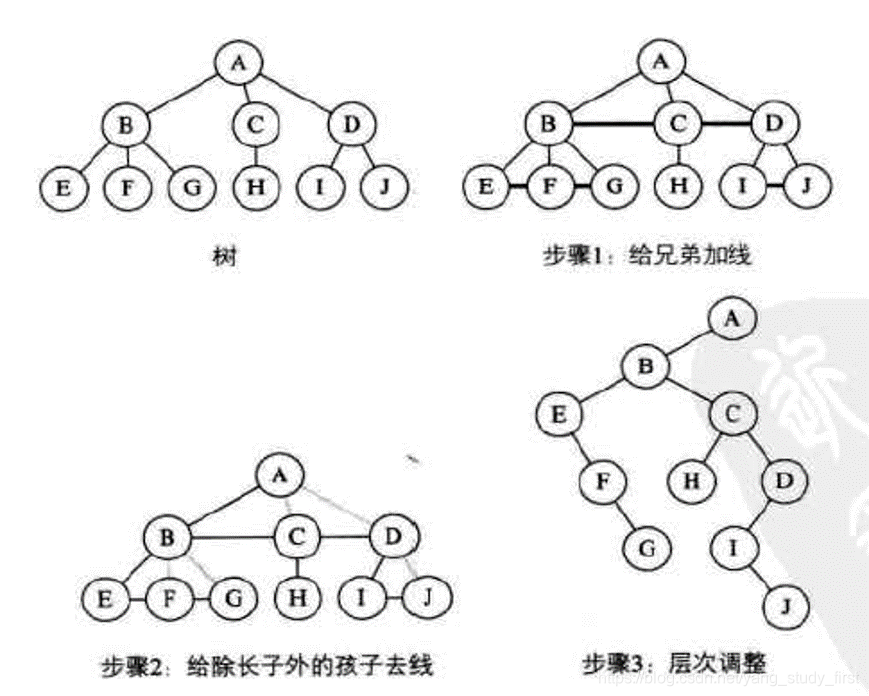
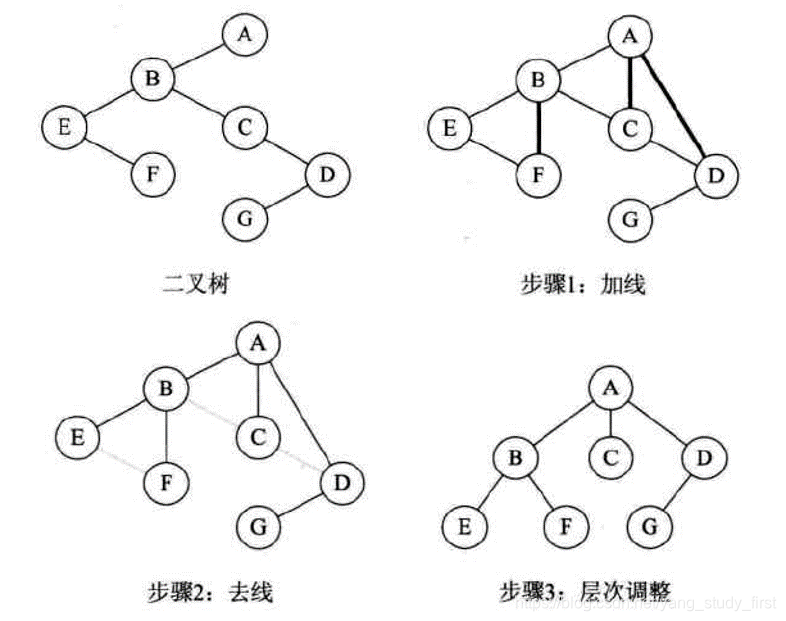
树转换二叉树
- 1、加线。在所有兄弟结点之间加一条连线。
- 2、去线。对树中的每个结点,只保留它与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
- 3、层次调整。以树的根结点为轴心,将整棵树顺时针旋转一定的角度,使之结构层次分明。注意第一个孩子是二叉树结点的左孩子,兄弟转换过来的孩子是结点的右孩子。
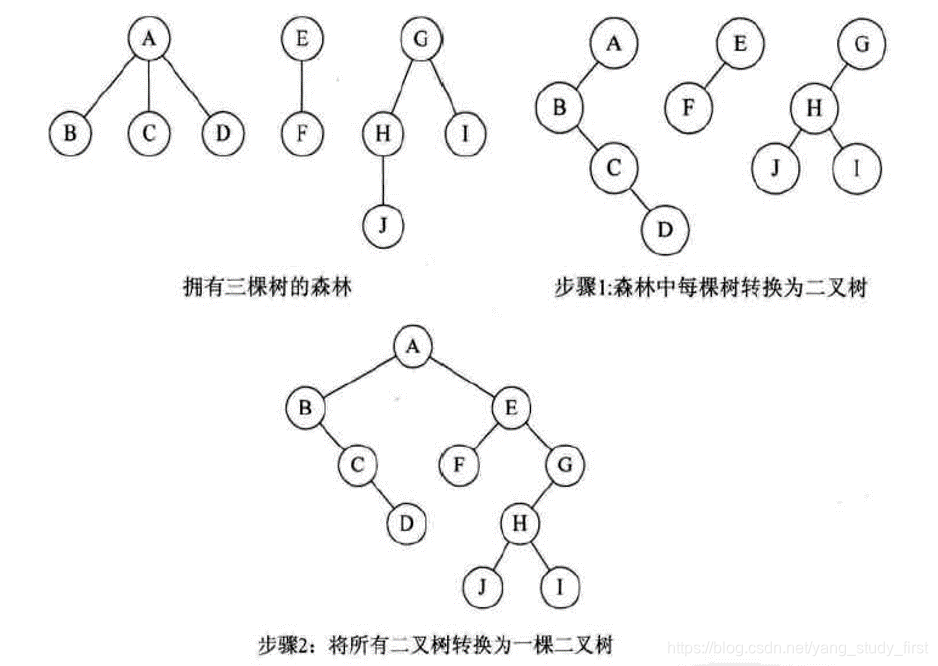
森林转换二叉树
- 1、把每个树转换为二叉树。
- 2、第一颗二叉树不动,从第二棵二叉树开始,依次把后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,用线连接起来。当所有的二叉树连接起来后就得到了由森林转换来的二叉树。
二叉树转换树
- 1、加线。若某结点的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点·······哈,反正就是左孩子的n个。
- 2、去线。删除原二叉树中所有结点与其右孩子结点的连线。
- 3、层次调整。使之结构层次分明。
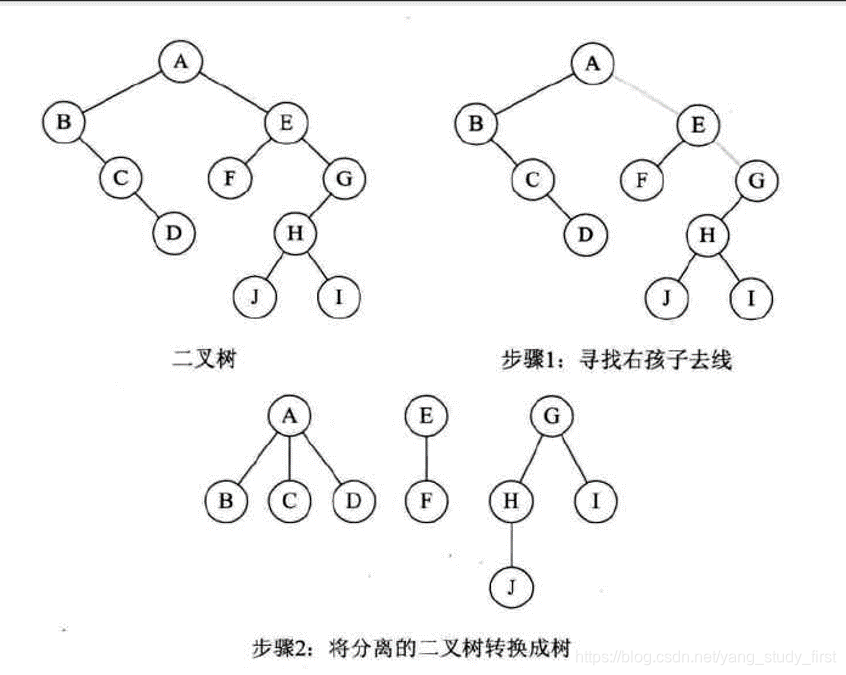
二叉树转换森林
- 判断一棵二叉树能够转换成一棵树还是森林,标准很简单,那就是只要看这棵二叉树的根结点有没有右孩子,有就是森林,没有就是一棵树。那么如果是转换森林,步骤如下:
1、从根结点开始,若右孩子存在,则把与右孩子结点的连线删除,再查看分离后的二叉树,若右孩子存在,则连线删除········,直到所有右孩子连线都删除为止,得到分离的二叉树。
2、再将每棵分离后的二叉树转换为树即可。
赫夫曼树
- 赫夫曼大叔说,从树中的一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的分支数目称为路径长度。在二叉树a中,根结点到结点D的路径长度为4,二叉树b中根结点到结点D的路径长度为2。树的路径长度就是从树根到每一结点的路径长度之和。二叉树a的树路径长度就为1+1+2+2+3+3+4+4=20。二叉树b的路径长度就为1+2+3+3+2+1+2+2=16。
- 如果考虑到带权的结点,结点的带权的路径长度为从该结点到树根之间的路径长度与结点上权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和。假设有n个权值{w₁,w₂,w₃,····,wn},构造一棵有n个叶子结点的二叉树,每个叶子结点带权wk,每个叶子的路径长度为lk,我们通常记作,则其中带权路径长度WPL最小的二叉树称作赫夫曼树。举例如下:

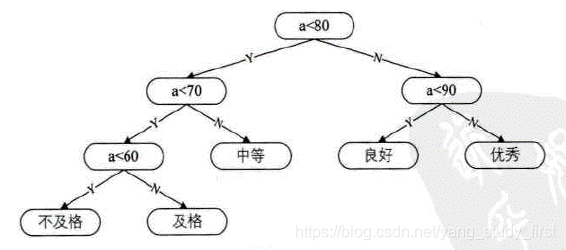
- 我们先把这两棵二叉树简化成叶子结点带权的二叉树,其中A表示不及格,B表示及格、C表示中等、D表示良好、E表示优秀。每个叶子的分支线上的数字就是刚才我们提到的五级分制的成绩所占比例数。
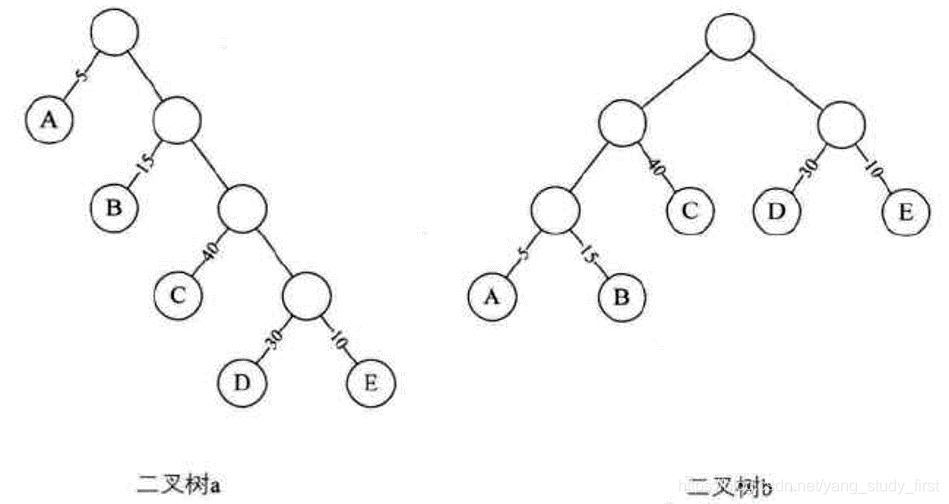
- 二叉树a的WPL=5×1+15×2+40×3+30×4+10×4=315
- 二叉树b的WPL=5×3+15×3+40×2+30×2+10×2=220
赫夫曼树的构造
- 1、先把有权值的叶子结点按照从小到大的顺序排列成一个有序序列,即A5,E10,B15,D30,C40。
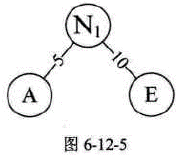
- 2、取头两个最小权值的结点作为一个新结点N₁的两个子结点,注意相对较小的是左孩子,这里就是A为N1的左孩子,E为N1的右孩子,如图6-12-5所示,新结点的权值为两个叶子的权值的和5+10=15。
- 3、将N₁替换A与E,插入有序序列中,保持从小到大排列。即N₁15,B15,D30,C40。
- 4、重复步骤2。将N₁与B作为一个新结点N₂的两个子结点。如图6-12-6所示。N₂的权值=15+15=30。
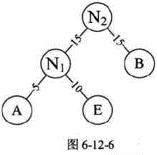
- 5、将N₂替换N₁与B,插入有序序列中,保持从小到大排列。即N₂30,D30,C40。
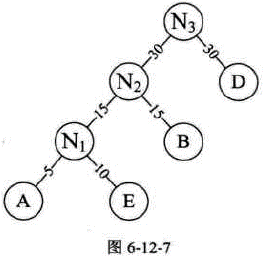
- 6、重复步骤2。将N₂与D作为一个新结点N₃的两个子结点。如图6-12-7所示。N₃的权值=30+30=60。
- 7、将N₃替换N₂与D,插入有序序列中,保持从小到大排列。即:C40,N₃60。
- 8、重复步骤2。将C与N₃作为一个新结点T的两个子结点,如图6-12-8所示。由于T即是根结点,完成赫夫曼树的构造。
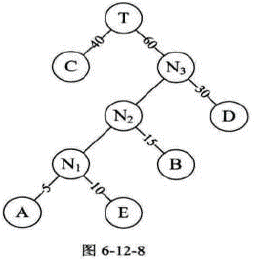
赫夫曼树构造过程
- 通过刚才的步骤,我们可以得出构造赫夫曼树的赫夫曼算法描述。
- 1、根据给定的n个权值{w₁,w₂,····,wn}构成n棵二叉树的集合F={T₁,T₂,·····,Tn},其中每棵二叉树T₁中只有一个带权为w₁根结点,其左右子树均为空。
- 2、在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
- 3、在F中删除这两棵树,同时将新得到的二叉树加入F中。
- 4、重复2和3步骤,知道F只含一棵树为止,这棵树便是赫夫曼树。
赫夫曼编码
- 当然,赫夫曼研究这种最优树的目的不是为了我们可以转化一下成绩。 他的更大目的是为了解决当年远距离通信(主要是电报)的数据传输的最优化问题。
- 比如我们有一-段文字内容为“ BADCADFEED”要网络传输给别人,显然用二进制的数字(0和1)来表示是很自然的想法。我们现在这段文字只有六个字母ABCDEF,那么我们可以用相应的二进制数据表示,如图6-12-2所示。

- 假设六个字母的频率为A27,B8,C15,D15,E30,F5,合起来正好是100%。那就意味着,我们完全可以重新按照赫夫曼树来规划它们。
- 图6-12-9 左图为构造赫夫曼树的过程的权值显示。右图为将权值左分支改为0,右分支改为1后的赫夫曼树。
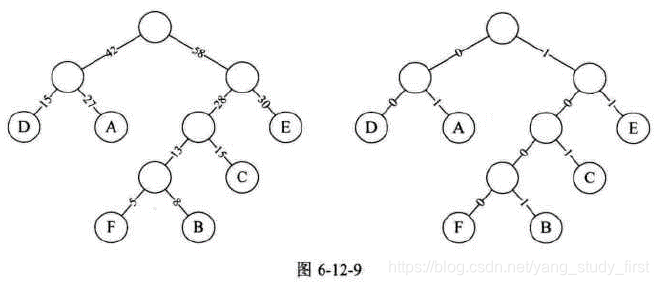
- 此时,我们对这六个字母用其从树根到叶子所经过路径的0或1来编码,可以得到如表6-12-3所示这样的定义。

- 我们将文字内容为“BADCADFEED”再次编码,对比可以看到结果串变小了。
- ■原编码二进制串 : 00100001101000011101100100011 (共 30个字符)
- ■新编码二进制串: 100101001010000111100 (共25个字符)
- 也就是说,我们的数据被压缩了,节约了大约17%的存储或传输成本。
二叉查找树
- 二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
代码实现
/**
* 创建查找二叉树,添加结点
*
* @param data
* @return
*/
public TreeNode put(int data) {
TreeNode node = null;
TreeNode parent = null;
if (root == null) {
node = new TreeNode(0, data);
root = node;
root = node;
}
node = root;
while (node != null) {
parent = node;
if (data > node.data) {
node = node.rightChild;
} else if (data < node.data) {
node = node.leftChild;
} else {
return node;
}
}
//表示将此结点添加到相应位置
node = new TreeNode(0, data);
if (data < parent.data) {
parent.leftChild = node;
} else {
parent.rightChild = node;
}
node.parent = parent;
return node;
}
/**
* 中序遍历
* @param node
*/
public void midOrder(TreeNode node) {
if (node == null) {
return;
} else {
midOrder(node.leftChild);
System.out.println(node.data);
midOrder(node.rightChild);
}
}
二叉树结点删除
- 分为四种情况,结点无左右子树(叶子结点);结点无左子树;结点无右子树;结点有左右子树。
- 1、删除的节点为叶子节点:直接删除。
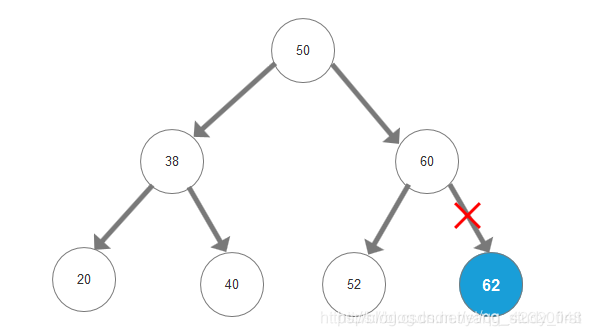
- 2、删除的节点只存在左子树或右子树:删除节点的父节点直接指向子树节点。
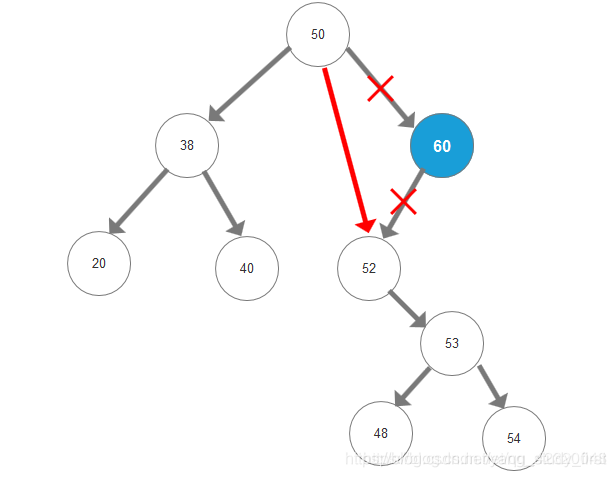
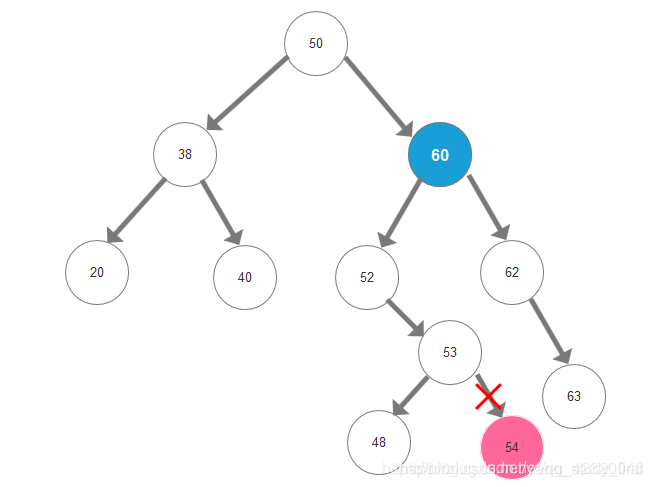
- 3、删除的节点同时存在左子树和右子树:将删除节点的左子树的最右节点或右子树的最左节点替换删除节点,同时删除替换节点,再将删除节点指向子树节点。
代码实现
//删除节点
public void Delete(DeleteBinaryTree root, int value) {
DeleteBinaryTree temp;
temp = Select(root, value);
if (temp.value == 0) {
System.out.println("你要删除的数值" + value + "不存在");
} else {
DeleteBinaryTree p = new DeleteBinaryTree();
DeleteBinaryTree node;
p = p.Select(root, value); //p是要删除的结点
node = p;
if (p != null) {
if (p.left != null) {
p = node.left;
while (p.right != null) {
p = p.right;
}
node.value = p.value;
if (node.left.right == null) {
node.left = p.left;
} else {
p.parent.right = p.left;
}
} else if (p.right != null) {
p = p.right;
node.value = p.value;
node.left = p.left;
node.right = p.right;
} else {
if (p.equals(p.parent.left)) {
p.parent.left = null;
}
if (p.equals(p.parent.right)) {
p.parent.right = null;
}
}
System.out.println("");
System.out.println("数据" + value + "删除成功");
}
}
}
二叉树结点修改
//修改节点
public void Update(DeleteBinaryTree root, int value, int update) {
DeleteBinaryTree temp = new DeleteBinaryTree();
temp = temp.Select(root, value);
if (temp.value == value) {
Delete(root, value);
DeleteBinaryTree a = new DeleteBinaryTree(update);
insert(root, a);
System.out.println("数据" + value + "成功更新成" + update);
} else {
System.out.println("数据" + value + "更新失败");
}
}























